Base Plate Design: Eurocode 3

Steel base plates are provided beneath steel columns in order to transmit the applied design forces safely to the foundations. Since steel columns are heavily loaded and their cross-sections are typically small, applying the loads directly on the foundation could result in a punching failure. Therefore a base plate must be provided beneath the column in order to spread the column load over a larger base area.

The actual distribution of pressure beneath a base plate is quite complex. EN 1993-1-8:2005 clause 6.2.5 and 6.2.8 presents a simplified approach. It assumes a uniform distribution of pressure beneath an effective area of the base plate known as the "equivalent T-stub in compression". The dimension, \( c \) in the figure below known as the "additional bearing width", forms an effective bearing area given by \( I_{eff} \times b_{eff} \).

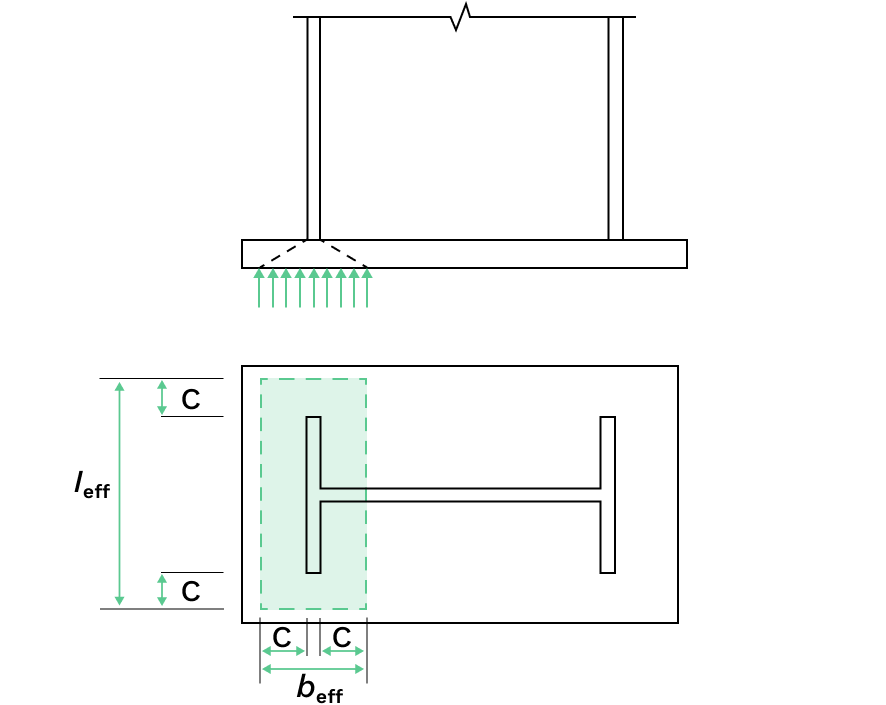
As per Clause 6.2.8.2, the capacity of a symmetric column base plate subject to an axial compressive force applied concentrically may be determined by adding together the capacities of the three T-stubs shown below (two T-stubs under the column flanges and one T-stub under the column web). The three T-stubs should not be overlapping.

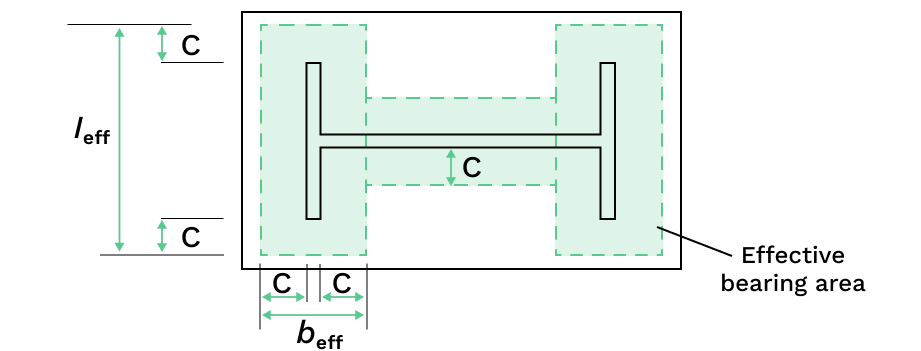
The required check is that the applied compressive stress on this effective area does not exceed the design bearing strength of the concrete support, \( f_{jd} \).

Let's walk through the steps for the "equivalent T-stub in compression" design method, which are based on a research paper from the University of Ahmadu Bello. It checks the bearing strength of the concrete support and determines the required width, length and thickness of your base plate.

Step 1: Compute the bearing strength of the concrete support, \( f_{jd} \)

$$ f_{jd} = \beta_j \times \alpha  \times\dfrac{\alpha_ {cc}f_{ck}}{ \gamma_c} $$

Where:

\( \rlap{\beta_j} \hspace{2.5em} \) : the foundation joint material coefficient, typically taken as 0.67 as per clause 6.2.5(7) in EN 1993-1-8.
\( \rlap{\alpha} \hspace{2.5em} \) : coefficient which accounts for the concrete bearing strength enhancement due the diffusion of the concentrated force within the foundation, as per clause 6.7 in BS EN 1992-1-1 (code also known as "EC2"). The value of \( \alpha=\sqrt{A_{c1}/A_{c0}} \) can be calculated directly if the dimensions of the concrete foundation is known. Otherwise, usual foundation sizes relative to that of the baseplate is shown to give \( \alpha\geq1.5 \) (source: SCIA Engineer).
\( \rlap{f_{ck}} \hspace{2.5em} \) : characteristic compressive strength of the concrete support
\( \rlap{\alpha_{cc}} \hspace{2.5em} \) : concrete coefficient for long-term effects, refer to your country's National Annex.
\( \rlap{\gamma_c} \hspace{2.5em} \) : partial factor of safety for concrete, refer to your country's National Annex.

The equation for \( f_{jd} \) above is not explicitly stated in the standards. Let's derive it together.

As per clause 6.2.5(7) in EN 1993-1-8:

$$ f_{jd}=\dfrac{\beta_{j}\times F_{Rdu}}{A_{c0}} \quad \text{where }  A_{c0}=b_{eff}\times I_{eff} $$

As per clause 6.7 in BS EN 1992-1-1:

$$ F_{Rdu}=A_{c0}\times f_{cd}\times \alpha $$

As per clause 3.1.6 in BS EN 1992-1-1:

$$ f_{cd}=\dfrac{\alpha_{cc}\times f_{ck}}{\gamma_c} $$

Putting these three equations together gives our final equation:

$$ f_{jd}=\dfrac{\beta_{j}\times [A_{c0}\times [\alpha_{cc}\times f_{ck}]/\gamma_c\times \alpha ]}{A_{c0}} \\ = \beta_j \times \alpha  \times\dfrac{\alpha_ {cc}f_{ck}}{ \gamma_c} $$

Step 2: Find the required area of the base plate, \( A_{req} \)

$$ A_{req} =\dfrac{N_{Ed}}{f_{jd}} $$

Where:

\( \rlap{N_{Ed}} \hspace{2.5em} \) : ULS design compression load from the column on the baseplate
\( \rlap{f_{jd}} \hspace{2.5em} \) : bearing strength of the concrete support

Step 3: Find the additional bearing width, \( c \)

The additional bearing width, \( c \) is obtained by equating the effective area, \( A_{eff} \) to the required rectangular area, \( A_{req} \). The equation for \( A_ {eff} \) is the sum of the effective areas of the three T-stubs (assuming no overlap), and is found using geometry.

$$\begin{gather}
& A_{eff}=4c^ {2}+ P_{col }\times c + A_{col} \\
& \rightarrow A_{eff}=A_{req} =\dfrac{N_{Ed}}{f_{jd}} \\
& \rightarrow 4c^ {2}+ P_{col }\times c + A_{col}-\dfrac{N_{Ed}}{f_{jd}} =0 \\
& \text{Solve for }c \end{gather}$$

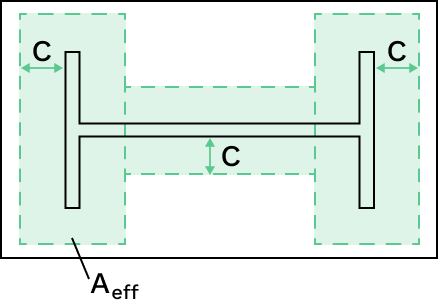
Step 4: Find the required base plate plan dimensions

Required baseplate width, \( w_p \) and length, \( l_p​ \) is given by:

$$\begin{gather}
& w_p=b+2c  \\
& l_p=h+2c \end{gather}$$

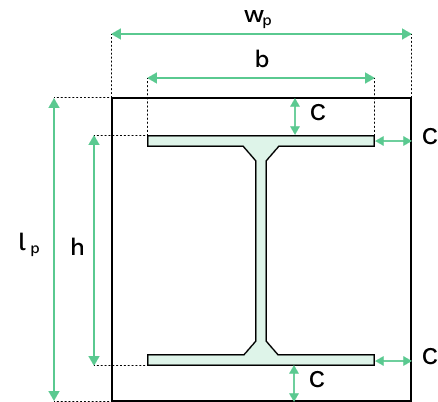
Note, as per EN 1993-1-8:2005 Section 6.2.5(5)&(6), if the baseplate has larger plan dimensions then required to fit \( c \), the additional projection beyond \( c \) is neglected from the effective bearing area.

Step 5: Calculate the required base plate thickness, \( t_p \)

Re-arranging the equation in clause 6.2.5(4) EN 1993-1-8 gives the required baseplate thickness:

$$ t_{p}=c\times \sqrt{ \dfrac{3 \times f_{jd}\times\gamma_{M0}} {f_y }} $$

Where:

\( \rlap{f_y} \hspace{2.5em} \) : yield strength of the T-stub (i.e. the steel baseplate)
\( \rlap{f_{jd}} \hspace{2.5em} \) : bearing strength of the concrete support
\( \rlap{\gamma_{M0}} \hspace{2.5em} \) : partial factor for resistance of cross-sections whatever the class is as per EN 1993-1-1, where the code recommended value is \( \gamma_{M0}=1.0 \)