Learn how to design a steel base plate, by checking the allowable bearing strength of the concrete footing and calculating the minimum required thickness of your base plate.
Introduction
What are base plates?
Steel base plates are used to distribute the load of a column or other structural member to a concrete foundation. Generally, a column base plate is made up of a plate and a minimum of four bolts.
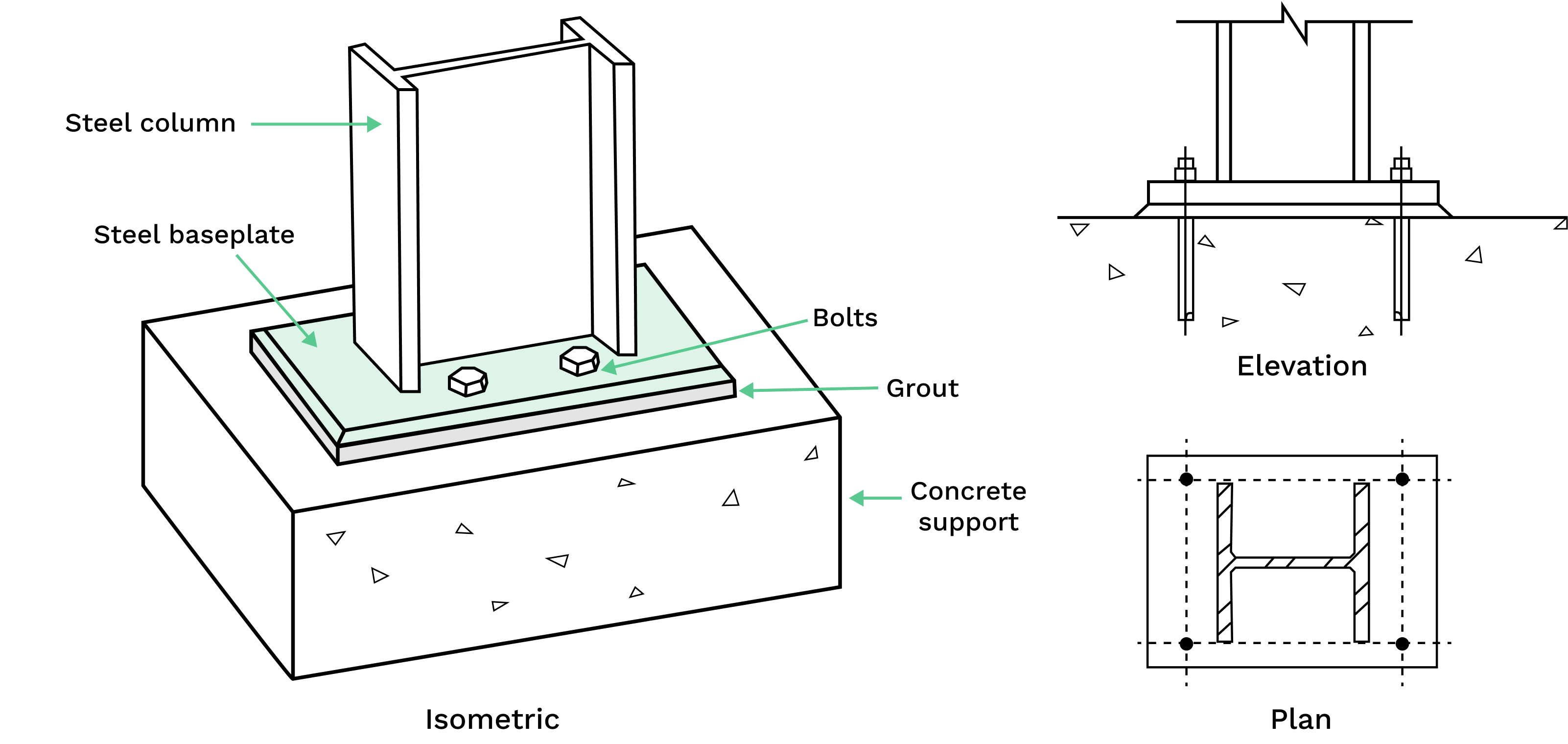
Base plates are typically made of ASTM A36 steel, which is a mild steel with good weldability and formability. They are also available in higher strength steels, such as ASTM A572 Grade 50, for applications where higher loads are expected.
Why are base plates used?
Base plates are used to:
- Distribute loads over a larger areas then the column cross-section. Concrete foundations are typically weaker than the steel column, but with the load distribution it will prevent concrete crushing.
- Level columns, to help ensure the column is vertical for the overall stability of the structure.
- Provide clearance between the column and foundation, to allow for drainage and prevents the steel column from corrosion.
What is the load path?
For the simple case of pure compression (no moments develop at the base plate), the load path is such that the column axial force is distributed from the column end to the column base plate in direct bearing. The column base plate is then assumed to distribute the column axial force to the concrete or masonry as a uniform bearing pressure by cantilevered bending of the plate.
Design approach according to AISC 360
There is two main design requirements: to design against crushing of the concrete footing by calculation of the footing's allowable bearing strength, and to determine the minimum base plate thickness by calculation of the "critical base plate cantilever length".
Check 1: Concrete Bearing Strength \( \frac{P_p}{\Omega_c} \)
The allowable bearing strength, \( \frac{P_p}{\Omega_c} \) is:
$$ \dfrac{P_p}{\Omega_c}=\dfrac{f_c^{\prime} A_1}{\Omega_c} \operatorname{min}\left[0.85\operatorname{max}\left(\sqrt{\dfrac{A_2}{A_1}}, 1\right), 1.7\right]\\\text{} $$
Where:
\( \rlap{P_p} \hspace{2.5em} \) : Nominal bearing strength of the concrete.
\( \rlap{\Omega_c} \hspace{2.5em} \) : Safety factor for compression. AISC 360-16 J8 outlines that in the absence of code regulations, the allowable bearing strength for the limit state of concrete crushing can be taken with the safety factor of compression, \( \Omega_c = 2.31 \).
\( \rlap{f_c'} \hspace{2.5em} \) : Specified minimum compressive strength of concrete.
\( \rlap{A_1} \hspace{2.5em} \) : Area of steel concentrically bearing on the concrete support.
\( \rlap{A_2} \hspace{2.5em} \) : Maximum area of the portion of the supporting surface that is geometrically similar to and concentric with the loaded area.
The design check then becomes \( P_a \leq \frac{P_p}{\Omega_c} \) where \( P_a \) is the design compression axial load.
Check 2: Minimum base plate thickness \( t_{min} \)
The design dimensions of the base plate \( m,n \) and \( n'\lambda\) are used to determine the critical base plate cantilever dimension \( l \) which is used to calculate the minimum base plate thickness \( t_{min} \).
.png)
The minimum required thickness of the base plate \( t_{min}\) is outlined in AISC Steel Construction Manual 14th Ed. 14-6 as:
$$ t_{min}=l\sqrt{\dfrac{3.33P_a}{F_yBN}} $$
Where:
- \( l =\) critical base plate cantilever dimension
- \( P_a= \) design compressive axial load
- \( F_y =\) base plat yield strength
- \( B= \) base plate width
- \( N =\) base plate depth
The critical base plate cantilever dimension is given by:
$$ l=\operatorname{max}(m,n,\ n'\lambda) $$
Where:
- \( n^{\prime}=\frac{\sqrt{d b}}{4}\)
- \( d= \) column section depth
- \( b =\) column section width
- \( \lambda=\operatorname{min}\left(\frac{2 \sqrt{X}}{1+\sqrt{1-X}},1\right) \)
- \( X=\operatorname{min}\left[\left(\frac{4 d b}{\left(d+b\right)^2}\right) \frac{\Omega_c P_a}{P_p}, 1\right]\)
- \( P_p =\) nominal bearing strength of concrete
The dimensions \( m \) and \( n\) vary based on the column section type:
$$ \begin{aligned} &\quad \text{Wide flange} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} m = \frac{N - 0.95d}{2} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} n = \frac{B - 0.8b}{2} \end{aligned} \quad\quad \begin{aligned} &\quad\quad \text{Tube} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} m = \frac{N - 0.95d}{2} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} n = \frac{B - 0.95b}{2} \end{aligned} \quad\quad \begin{aligned} &\quad\quad \text{Pipe} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} m = \frac{N - 0.8d}{2} \\ &\vphantom{\frac{\frac{0}{0}}{\frac{0}{0}}} n = \frac{B - 0.8d}{2} \end{aligned} $$
.png)
