Structural Load Calculations

Defining and calculating load combinations is essential in structural design to ensure their safety and stability. This process involves identifying all potential loads a structure may encounter, analyzing their effects, and applying appropriate safety factors and load scenarios in simulation models.

Design loads include the self-weight of the structure, the weight of occupants, wind, snow, seismic forces, and any semi-permanent elements, materials, or equipment used during construction or operation. Engineers must determine suitable design load combinations to develop structures that meet strength and serviceability requirements. These combinations help ensure the structure can resist impacts and avoid fatigue failure over time.

Design codes in varying geographical jurisdictions with each offering specific recommendations for load combinations. These variations are due to specific features of the environment as well as the principles of local regulatory bodies.

This article provides an overview of design load calculations and combinations as outlined in AS/NZS 1170:2002, ASCE 7-10 and EN 1991-1-1, highlighting similarities and differences among these widely-used standards.

What are structural loads and how do you calculate them?

A structure can be affected by various loads, which depend on factors such as its design, location, and intended use. In most cases, the maximum loads a structure must withstand are used to define design requirements. Structural loads are commonly classified into dead loads (DL) and live loads (LL).

\( \bf{1.1} \) Dead Loads

Dead loads on a structure are always present and cannot be removed. As such, structure must be designed to safely support the weight of its own dead loads.

Often referred to as permanent loads, dead loads remain constant over time. Examples include the self-weight of a building's structural elements, flooring components and finishes, building services and operational equipment, like the HVAC system, non-structural permanent partitions, immovable fixtures, and even built-in cabinets.

Most dead loads can be calculated by assessing the weights and volumes of specified materials, as indicated in drawings or measured in situ, and considering the areas over which they are distributed. This method allows for accurate calculations of dead loads.

Structural engineers also tend to be conservative in their estimates, minimizing acceptable deflections, allowing margins of error, and accounting for potential changes in conditions over time. As a result, designed dead loads frequently exceed actual loads.

\( \bf{1.1.1} \) Calculating dead loads

By calculating the volume of each member and multiplying it by the unit weight of the materials from which it is composed, an accurate dead load can be determined for each component.

$$ \text{Dead load} = \text{Volume of member} \times \text{Unit weight of material} $$

The different components can be added together to determine the total dead load.

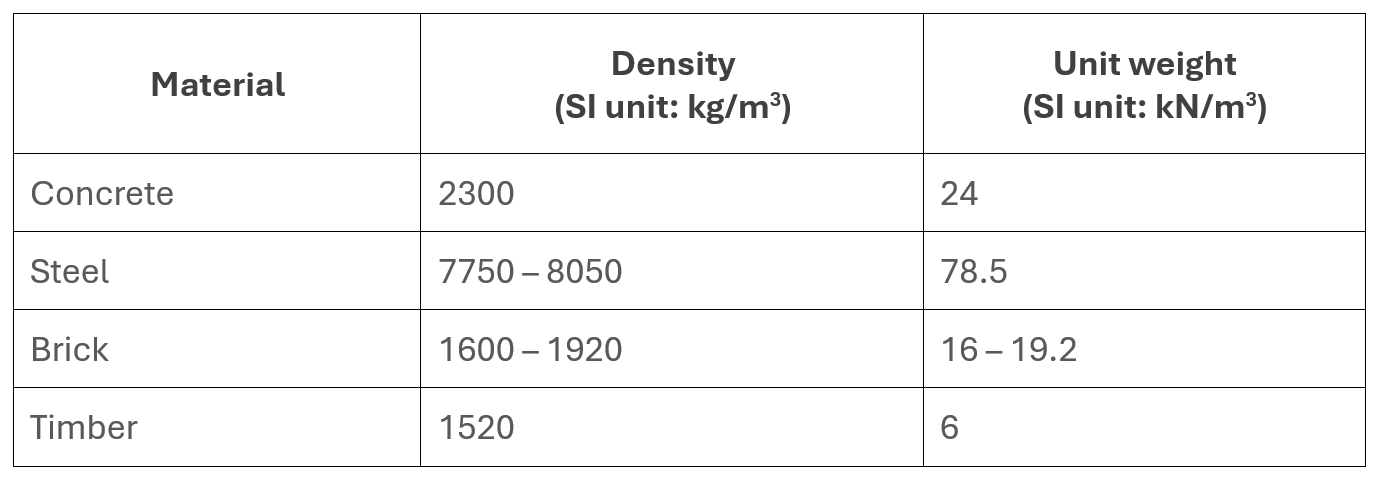
In most instances, engineers will translate loads into a UDL (uniformly distributed load), measured in kilopascals (kPa) or pounds per square foot (psf), and an equivalent allowable concentrated loads (point loads). Dead load UDLs will be combined with superimposed loads and live loads to calculate the ultimate and service loading conditions on the structure.

\( \bf{1.1.2} \) Superimposed Dead Loads (SDLs)

SDLs are permanent loads added to a structure, but not part of the structure itself. Examples include movable partitions, planter boxes, fixed office equipment, and base building systems such as mechanical and electrical systems. While these loads are generally constant, they can be relocated during renovations.

Similar to pure dead loads, SDLs are presented as a UDL and are used generally in a design. An important distinction between pure dead loads and SDLs is that SDLs are sometimes treated as allowable loading for architects and building occupants.

DL and SDL are typically combined and referred to as a total dead load, or sometimes referred to as G in structural engineering codes and calculations.

\( \bf{1.2} \) Live Loads

Live loads, also known as applied or imposed loads, are temporary and subject to change over short periods. They vary in location and magnitude and include the weight of people, furniture, vehicles, and other moveable objects. A structure must be designed to safely support the weight of the maximum possible live loads it may be subjected to. Common examples of live loads include the weight of audiences in an auditorium, the books in a library, and traffic on bridges.

Given the dynamic nature of live loads, they are rarely calculated from scratch, unlike dead loads. Instead, they are determined based on design codes, which specify rates and allowable loading requirements.

Typical live load values for different building purposes can be found in tables within building codes, such as:

EN 1991-1-1 (Table 6.1 + Table 6.2)
AS/NZS 1170.1:2002 (Table 3.1)
ASCE/SEI 7-10 (Table 4-1)

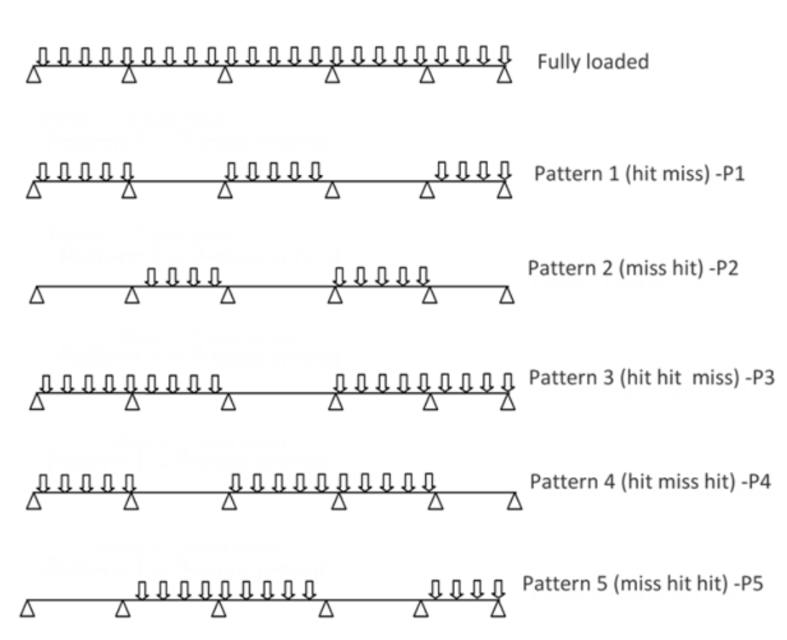
\( \bf{1.2.1} \) Pattern Loading

Engineers consider the worst-case scenario for a structural member at any given loading scenario. For live loads, this requires engineers to consider pattern loading, where loads aren’t evenly distributed, as varying loading arrangements may increase design loads on structural elements.

The diagram above show some examples of different loading patterns along a continuous beam with five sections. In these scenarios, not all members are subjected to the same loading at a given time. For a continuous beam, this may increase hogging moments, which must be factored into the design.

Different building codes require different sets of pattern loads and depth of analysis. Engineers should pay attention to the dynamics of expected live loading on structures they design.

Environmental loads, such as seismic movement, wind, waves, rain, and snow, can impact structures in a short time frame similar to live loads. However, they have specific calculation protocols and loading rules and are considered separate from live or dead loads as they may act horizontally and dynamically.

Regional differences greatly affect environmental loads. Climate, topography, and seismic activity vary from region to region, causing loading requirements to differ. For instance, Christchurch, New Zealand has stricter seismic loading rules than London, England.

\( \bf{2.1} \) Snow Loads

Snow loads arise from the weight of accumulated snow and ice on a roof. If this load exceeds the structure's capacity, the roof or the entire structure may fail. Codes for snow load standards include:

AS 1170.3:2002
ASCE 7-16
EN 1991-1-3
NBCC 2015 Section 4.1.6

‍

\( \bf{2.2} \) Wind Loads

The wind is a mass of air that moves mostly horizontally from a high-pressure region to a low-pressure region. Wind load is the intensity of pressure, i.e. the load, in pounds per square foot, placed on the exterior of a structure by the wind. High winds can cause a lot of damage because they pressure a building's surface.

This will depend on the:

• angle at which the wind strikes the structure
• structure’s shape and size
• placement of items like antennas mounted on the structure
• design and construction of the structure

Codes for wind load standards include:

AS/NSZ 1170.2
ASCE 7-16 Section 26
EN 1991-1-4 Section 5

Specialised wind analyses involving computational fluid dynamics (CFD) or wind tunnel experiments may be conducted for critical structures like hospitals to provide structural designers with more accurate wind-loading data.

\( \bf{2.3} \) Seismic Loads

Seismic loads account for earthquake-induced forces. They are calculated according to the international building code, and they tell how much seismic energy a structure needs to withstand.

The following factors are considered when calculating seismic loads:

• earthquake parameters at the construction site
• type of materials used to build the structure
• quality of a structure's construction

Steps to determine seismic loading:

The seismic load can be calculated by multiplying the Total Seismic Weight by the seismic response coefficient C_s in a horizontal direction. The general steps to determine seismic loading are as follows:

1. Define building parameters (Geometry, importance level, occupancy category, etc.). The exact metrics will depend on the code you’re using.
2. Define site parameters (Seismicity zone, site adjustment factors, importance factor, etc.)
3. Define structural design parameters (based on the structural system selected, ductility, diaphragm flexibility, redundancy factors, etc.)
4. Compute seismic mass and resultant loads based on the defined parameters. Ensure to include torsional loads as applicable in your structure.

Codes for seismic load calculations include:

AS/NSZ 1170.4
ASCE 7-16 | Table 12.2 - 1
EN 1998-1
NBCC-2005, 2010, 2015

To ensure safety under various scenarios, building codes typically specify a variety of load combinations along with load factors (weightings) for each type of load.

Codes for combinations and associated load factors include:

ASCE 7-10 Section 2.3.2, 2.4
ACI 318-08 Section 9-2aa
EN 1990:2002, Section 6 - Table A1.2 - A1.4
AS/NZS 1170.0:2002 Clause 4.2.2

For example: AS1170 1170.0 - Clause 4.2.2 shows what determines the loading combination used in strength analysis (as opposed to serviceability). They involve commonly considered loads such as dead loads, live loads, and wind action.

Multiple combinations of relevant loads experienced by structural members are calculated and the highest calculated load combination determines the governing design load.

Understanding building codes and standards is important to ensure that the structures are safe, functional, and address user needs. These codes provide a set of minimum requirements to protect public health, safety, and welfare. They also ensure that structures are durable, energy efficient, and capable of withstanding natural disasters and other hazards.

Engineers who understand building codes and standards can design structures that meet these requirements, anticipating potential issues and mitigating risks. This can help to prevent costly errors and delays during construction, ensuring that the finished structure is fit for its intended purpose.

\( \bf{4.1} \) Fire Rating

Structures are required to withstand fires for a specified duration. They are also expected to maintain compartmentalization such that fires are contained locally within the building to a small group of rooms or floors.

AS 1530.4:2014 Clause 2.12.2 outlines that structural adequacy of elements exposed to fire is recorded for failure in the following aspects:

• excessive deflection of structural elements under heating
• detachment of structural elements
• structural collapse
  

Based on these failure criteria, the Fire Resistance Level (FRL) is determined by the amount of time in minutes that a structural member can last before it fails the criteria. The FRL is expressed as ‘adequacy/integrity/insulation’. If a structural element has an FRL of 30/60/90, then it means the element is within the adequacy criteria for 30 minutes, integrity criteria for 60 minutes, and insulation criteria for 90 minutes before failing. If a criterion is inapplicable, the value will take the form of a dash (i.e. –/60/90, 30/–/90, or –/60/90).

\( \bf{4.2} \) Robustness

In construction, robustness describes the ability of an overall structure to withstand events such as extreme loading, fire, explosions, wind, and other loading effects without losing its core functionality. The relevant codes for structural robustness are:

AS1170.0 Section 6
EN 1991-1-7
ASCE 7-02

Among these, only the Australian Standard provides specific requirements for structural robustness in terms of load resistance. The Eurocodes and US standards offer general provisions and design guidelines for such events without explicit mentions of robustness.

AS1170.0 Section 6 outlines loading requirements to ensure the structural system can withstand extreme events. Clause 6.2.2 requires that the lateral resistance of a structure and its connections must meet a specified percentage of the design loads of members at each floor level. The purpose of these lateral load resistances is to direct load paths across the structure to its foundations.

For hyper-critical structures, engineers should also understand alternate load paths to avoid systemic collapse. This ensures that if one structural element fails, it does not lead to the catastrophic failure of the entire structure. Failures of this kind can result from fabrication, manufacturing, or construction defects, with potentially devastating consequences such as the pancaking of Christchurch buildings in the 2010 Canterbury Earthquake. By designing alternate load paths that meet the lateral and connectional resistance requirements specified in Clause 6.2.2, engineers can significantly enhance a structure's robustness and safeguard against such collapses.